The Problem with Chutes and Ladders
“Chutes and Ladders” is an old children’s game where players take turns spinning a spinner and moving their pawn between one and six spaces. Throughout the board of 100 spaces are nine ladders and ten slides (chutes?) that transport your pawn up or down. There are little illustrations describing why you were rewarded with a ladder (doing your chores, helping a wounded puppy, etc.) or punished with a slide (skating on thin ice, making a mess, etc.).
I played this game when I was young, and my own son plays it now. When he was three and four, the game helped him learn to count, and perhaps taught him some good behavior.
But when my son turned five, the game just got…boring, for me at least. There is no strategy to “Chutes and Ladders”: All we do is spin, move, spin, move until my son performs his victory dance or, if I am unlucky enough to actually win the game, he demands a rematch. To make things worse, if we are both sufficiently unlucky (by landing on numerous slides), the game can last a very long time.
But just like a senior citizen at the bingo parlor, my son is hooked, and there is no denying a five-year-old when he wants to play “Chutes and Ladders”. So I spin, move, spin, move until my mind wanders and I contemplate the finer points of the game.
For example, I always let my son go first. I wondered what advantage this gives him? (A big one, I hoped!) Calculating the answer requires playing lots of games. Luckily, R can play “Chutes and Ladders” a lot faster than we can.
Simulating the Game
The first step is to create the board. The following matrix is helpful:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
chutes_ladders<-matrix(c(1:100,1:100),nrow=100,ncol=2) ##ladders chutes_ladders[1,2]=38 chutes_ladders[4,2]=14 chutes_ladders[9,2]=31 chutes_ladders[21,2]=42 chutes_ladders[28,2]=84 chutes_ladders[36,2]=44 chutes_ladders[51,2]=67 chutes_ladders[71,2]=91 chutes_ladders[80,2]=100 ##slides chutes_ladders[16,2]=6 chutes_ladders[49,2]=11 chutes_ladders[62,2]=19 chutes_ladders[87,2]=24 chutes_ladders[48,2]=26 chutes_ladders[56,2]=53 chutes_ladders[64,2]=60 chutes_ladders[93,2]=73 chutes_ladders[95,2]=75 chutes_ladders[98,2]=78 |
Now, R plays the games. 10,000 games run in about 5 minutes on my laptop, and provides plenty of data.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
library(data.table) games<-data.table(x=integer(),y=integer(),number=integer(),winner=character(),turns=integer()) total=10000 set.seed(1) pb <- txtProgressBar(min = 0, max = total, style = 3) for (g in 1:total){ x=0 y=0 game<-data.table(x=integer(),y=integer(),number=integer()) while(!(x==100|y==100)){ s<-sample(1:6,1) if (x+s<101){ x=x+s } x<-chutes_ladders[x,2] s<-sample(1:6,1) if(y+s<101){ y=y+s } y<-chutes_ladders[y,2] turn<-data.table(x=x,y=y,number=g) game<-rbindlist(list(game,turn),use.names=FALSE,fill=FALSE) } if(x==100){ game$winner<-"x" } else if(y==100){ game$winner<-"y" } game$turns<-nrow(game) games<-rbindlist(list(games,game),use.names=FALSE,fill=FALSE) setTxtProgressBar(pb, g) } close(pb) |
The result is a data table called “games” that contains all the moves for each of the 10,000 games played. I’ve also recorded the number of turns in each game and the winner, either “player x” or “player y.”
First-Mover Advantage
What advantage is afforded the player who goes first? There are no “ties” in “Chutes and Ladders”, so the first-player advantage lies in situations where the second player could have tied on the last turn. The simulation above gives each player an equal number of turns, but awards the first player (player x) the victory in the case of a tie. In a real game, the second player (player y) wouldn’t even spin because the game would be over, but the result is the same.
|
1 2 |
ties<-games[x==100&y==100] nrow(ties) |
156 games were awarded to player x that could have ended in a tie. Assuming that player x should only have been given credit for half those games, player x has a 50.78% chance of winning each game. Not much of an edge, there.
Do Cheaters Prosper?
My son tries to give himself an edge sometimes by, ahem, cheating. At the beginning of the game, he’ll control the spinner so that it lands on “one” so he is awarded a ladder that starts on space one and transports his pawn to space 38. Another of his strategies is to (ahem) “make sure” he lands on the biggest ladder, which stretches from space 28 all the way to space 84. He is convinced that landing on the biggest ladder is a sure path to victory and he’ll “miscount” his pawn’s moves in order to experience the sublime thrill of ascending to the upper reaches of the board. Having played many games of “Chutes and Ladders”, I know that a player who is far behind can actually have a run of luck and win, so I sometimes wonder what kind of advantage those two cheats really give my son. First, let’s consider spinning a one to start the game:
|
1 2 3 4 5 |
games_won<-games[!duplicated(number)] x_spins_1<-games_won[x==38&!y==38] x_spins_1_count<-x_spins_1[,.N,by=winner] x_spins_1_count[,percent:=N/sum(N)] x_spins_1_count |
If player x spins a one to start the game and the other player does not, player x wins 55.5% of the time.
And the biggest ladder? This code is a bit more complicated because we subset moves that landed on space 84, and then determine which of these turns were the result of the biggest ladder by looking at the previous turn:
|
1 2 3 4 |
x_space_84<-games[,previous:=shift(x,n=1,type="lag")][x==84] biggest_ladder<-x_space_84[previous<78] biggest_ladder_count<-biggest_ladder[,.N,by=winner][,percent:=N/sum(N)] biggest_ladder_count |
If player x lands on the biggest ladder at some point in the game, he wins 60% of the time.
So, my son’s “cheating” is helping him, but less than he realizes. I think this is because the creators of the game placed enough random slides and ladders throughout the board to keep any one move from ensuring victory. I’m told this game is 1000 years old, and I would wager that kids back then cheated too.
Root Cause
The game wouldn’t be very exciting for my son if he won every time, anyway. The real cause of my boredom is the length of some games. Inevitably, the clock is drifting past bedtime, and there we are – spin, move, spin, move – all the while I am hoping I don’t win. (I really shouldn’t complain, my son is great and I love to spend time with him. But spin, move, spin, move is not exactly a bonding moment.)
The following code creates descriptive statistics about the length of the games:
|
1 2 3 4 |
mean(games_won$turns) hist(games_won$turns,breaks=100) min(games_won$turns) max(games_won$turns) |
 In the simulation, an average game lasts 26.5 turns, but it is a right-tailed distribution, so the longest game lasted 146 turns!
In the simulation, an average game lasts 26.5 turns, but it is a right-tailed distribution, so the longest game lasted 146 turns!
A few notes for the mathematically inclined: 1) The length of the game is theoretically unbounded because there is a chance, no matter how small, that both players will be cursed and land on slides forever. 2) I ran this simulation 10 times to make sure that 10,000 games produced a representative average length. It did: The mean of means was 26.49909 with a standard deviation of 0.1533848 3) There are some more sophisticated measurements of the average game length that employ Markov Chains here and here.
If only there was a way to give each game a more consistent and shorter length.
Then, it hit me. There are nine ladders and ten slides. There is a ladder missing! What if I placed a new tenth ladder on the board that consistently shortened the game? Yes, but where?!
Creating a New Ladder
The following code counts all the times each space of the board was landed on in the simulation.
|
1 2 |
All_moves<-data.table(all=c(games$x,games$y)) All_moves_count<-All_moves[,.N,by=all][order(-N)] |
Reviewing the 15 most popular spaces, most are either on a ladder or a slide. This makes sense, as there are two ways to land on each of these spaces. But one space is not, space 47. This space precedes the dreaded “double slide” of spaces 48 and 49, the two spaces every child yearns desperately to skip over with a high spin.
Googling images of “Chutes and Ladders” game boards, I have noticed that on older versions of the game, sometimes called “Snakes and Ladders”, the slide on space 48 on my version starts on space 47. If this is the case on your board, replace the line chutesladders[48,2]=26 with the following: chutes_ladders[47,2]=26.
What if space 47 was the beginning of a ladder that stretched all the way to space 100?
Before you object, consider that that space 80 has just such a ladder, and players win that way all the time. Run the following code to confirm that about half of all games end with the winner landing on space 80:
|
1 2 3 |
x_wins<-games[,previous:=shift(x,n=1,type="lag")][x==100] x_wins[,space_80:=previous<94] x_wins_count<-x_wins[,.N,by=space_80][,percent:=N/sum(N)] |
So, adding another winning ladder on space 47 isn’t such a big deal.
The following line of code creates the ladder:
|
1 |
chutes_ladders[47,2]=100 |
Again, if your version already has a ladder on space 47, use the following code: chutes_ladders[48,2]=100
Now, re-run the simulation and produce the same descriptive statistics on the length of the game. Now, an average game lasted only 15.2 turns, and the longest game in the simulation lasted 106 turns.
|
1 2 3 4 5 |
games_won<-games[duplicated(number)] mean(games_won$turns) hist(games_won$turns,breaks=100) min(games_won$turns) max(games_won$turns) |
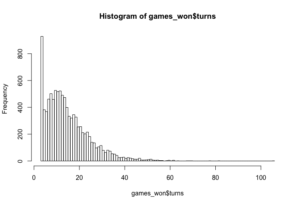
Unfortunately, this hack creates an explosion of games that end in three turns (see the histogram). Here’s how it happens: a player spins a one to start the game and ends up on space 38. Two lucky spins later, he lands on space 47 and wins. (My son’s cheating would pay off handsomely in this version of the game). The other problem is purely aesthetic: a ladder stretching across the board in this way would cover at least two of the illustrations.
To make a more subtle change to the game, have the new “space 47 ladder” end at space 72. The player who climbs this ladder has 1/6 chance of winning the game within two turns by landing on space 80. The mean in the simulation decreased to 22.4, the longest game was 110 turns, there are no more three-turn games, and the ladder doesn’t even cover any illustrations. Most importantly, there would be on average of 15% more “game time” we can spend playing Legos!
Conclusion
In the end, the solution to making “Chutes and Ladders” more enjoyable for adults is to spend a little time creating a paper ladder and taping it to the board. And your kids might get a kick out of the new ladder as well.

I love this article, because it puts solid analysis behind one of my most common gripes about this kind of kid’s game. Candyland, sorry! and Trouble are also offenders.
Length is a problem, but the biggest issue for me is lack of choice. I developed with my son a game that is topologically similar to Chutes & Ladders, but it contains game mechanisms that turn it into a light strategic game. Without going too in-depth, player movement is done by selecting a number card from a limited hand of cards. I would recommend buying a set of blank playing cards online, numbering about 24 of them 1-6, shuffling them, dealing 2 to each player. On your turn, select which card you will play and then draw a new one. You may need to make it a hand of 3 to make the choice meaningful, but I am away from my prototype kit and cannot test it.
The standard play rules of Sorry! do allow for a small amount of player choice (e.g. which piece to move, how to split a 7, whether to move 10 forward or 1 backwards, which opponent to send back to Start). This is increased significantly by the alternative rules included with the set where, as in your game, the players are dealt a small number of cards initially and on each turn, choose one to play, drawing a replacement from the deck.
Interesting idea! Feel free to repurpose the code in this article to build your own simulation.
Hi Ethan,
Great write-up and empirical analysis. This post caught my eye, because I once did a theoretical analysis project on Chutes and Ladders, using Markov chains. The great strength of the Markov chain is that given an arbitrary start state (board position), you can calculate the probability of achieving an end state (game finish) in a certain number of steps. So, when you know the position of all players on the board, you are able to determine which is most likely to win, and how many more turns the game is likely to last. This accounts for the fact that a player on square 75, for example, has a much greater probability of winning the game than a player on square 92, and even allows you to calculate the exact probabilities involved.
Also interesting, and mentioned in your article, is that while a game can technically go on forever, the configuration of the chutes and ladders determines the average number of turns it takes to finish the game. If the chutes and ladders are redefined and redistributed, the dynamics of the game can be tailored as you see fit (e.g. indroducing a ladder from 1 to 100 will result in a p/6 chance the game will end in a player’s first turn, given p players).
Thank you. Yes, I believe I provided a link to your interesting article in one of my notes. Feel free to post a link in the comments as well.
Sir, I object to you calling Chutes & Ladders a “game”. A game has decisions, strategy or skills needed to, well, make it a game. C&L lacks all of these and is therefore an “activity,” not a game. I do approve of you coming up with a solution to shorten the activity. Try to remember this when your son graduates to Monopoly, another that really has no decisions; your “hack” – all house rules must shorten play. 🙂
Yes, the “kids” version of Monopoly requires the player to buy a property if you have the opportunity, removing the one strategic decision from the original “game”, thus demoting it to an “activity.” Good idea for a future post!
Another simple way to add choice to the game is letting the player decide whether or not to go up a ladder when they land on it. Which allows strategies like avoiding a ladder that lets out in a region with a lot of chutes and instead hoping to take a later ladder that avoids such a region. Or the inverse strategies for Dad. 😉
So I had a little time and wrote the same simulation of yours in ruby and am able to simulate 100M games in about 19 minutes with Rubinius. 76m with the standard MRI.
https://github.com/twohlix/chutes_and_ladders if you want to play with the ruby version 🙂
Interesting read otherwise.
Thank you for “porting” my work to Ruby! It does appear that Ruby is far more efficient performing this kind of simulation. That said, you’ll see in the notes that I ran 10,0000 simulations 10 times, and found the mean relatively unchanged. So, in this situation, R is good enough. (I think experienced R coders would point out that it is possible to write the code in C and run it in R, which might yield even better performance than Ruby).
Sure, it was just a fun problem to replicate. Also Ruby not Python, but yes 10k is good enough. Although you only saw 146 as your longest game in 10k games but I’ve seen a 263 turn win in a sim of 1M where all 1M games were won, and as we know there is no technical upper limit to the number of turns it could take. With a limit of 150 turns I see around 100 games out of 1M that would last longer than 150 (aka not won games).
Outliers can be fun too! I think my simulations have almost proven through brute force that its impossible to win in 6 turns on this board while a 10k sim cannot. You’d need to attempt 46,656 games to try all the rolls possible for a 6 turn game (6^6). While I realize my sim could have missed that one set of ‘perfect rolls’ for the 6 turn game, in 300M+ games not having seen that 6 turn game starts to lend some evidence that its impossible. I believe its a 1 in 2143 chance I missed that set of rolls in 100M games.